The Vuvuzelas used during the 2010 FIFA World Cup in South Africa caused complaints from TV viewers and broadcasters due to their loud and monotonous sound, which can induce hearing loss. To improve commentary clarity, frequency selective filtration can be applied, but it is challenging as Vuvuzela's frequency is similar to speech tone, making it necessary to avoid dampening commentators' voices.
Solution
The choice of filter to remove vuvuzela noise ultimately depends on the specific characteristics of the audio signal and the desired level of noise reduction. However, in general, a Wiener filter is typically more effective than a Butterworth Band Stop filter for removing vuvuzela noise.
A Butterworth Band Stop filter is a type of frequency-selective filter that attenuates a specific range of frequencies. In the case of vuvuzela noise, the filter would need to attenuate the frequencies in the range of the vuvuzela sound (typically around 200-400 Hz). While a Butterworth Band Stop filter can be effective in attenuating the vuvuzela noise, it may also attenuate other important frequency components of the audio signal, resulting in a distorted or muffled sound.
On the other hand, a Wiener filter is a statistical signal processing technique that estimates the underlying signal from a noisy observation. It is designed to minimize the mean square error between the original signal and the denoised signal, giving an estimate of the noise power spectral density. A Wiener filter can effectively remove vuvuzela noise while preserving the important frequency components of the audio signal, resulting in a clearer and more natural-sounding output.
A. Using Butterworth Band Stop Filters
A Butterworth Band Stop filter is a static filter. A static filter is a filter with fixed coefficients that do not change based on the input signal. In the case of the Butterworth Band Stop filter, the filter coefficients are determined based on the desired frequency response of the filter, which is specified by the filter order and the location of the stopband. Once the filter coefficients are determined, they remain fixed and do not change based on the input signal.
Procedure:
1. Combine the original audio clip with the Vuvuzela clip to create a distorted audio clip.
2. Convert the distorted audio clip from the time domain to the frequency domain using MATLAB software.
3. Plot a graph of power against frequency to identify the frequencies with higher power than usual.
4. Note down the frequencies above a specified threshold value of 1x104W as these are the ones generated by the Vuvuzela trumpet.
5. Design 13 bandstop filters, one for each of the 13 identified frequencies, to remove those frequency components from the distorted audio clip while keeping other frequencies intact.
6. Use the graphical user interface of MATLAB to design each band stop filter for a specific frequency or range of frequencies.
7. Combine all the band stop filters and implement them on the distorted audio clip to obtain the desired output without the Vuvuzela noise.
The static nature of the Butterworth Band Stop filter means that it is effective for attenuating fixed frequency components of the input signal, such as the vuvuzela noise in an audio recording. However, it may not be as effective for adapting to changes in the noise characteristics over time, or for preserving the important frequency components of the signal while attenuating the noise.
Therefore the choice of filter depends on the specific characteristics of the input signal and the desired level of noise reduction. While a Butterworth Band Stop filter can be effective for attenuating specific frequency components of the signal, an adaptive filter like the Wiener filter may be more effective for reducing noise while preserving the important frequency components of the signal.
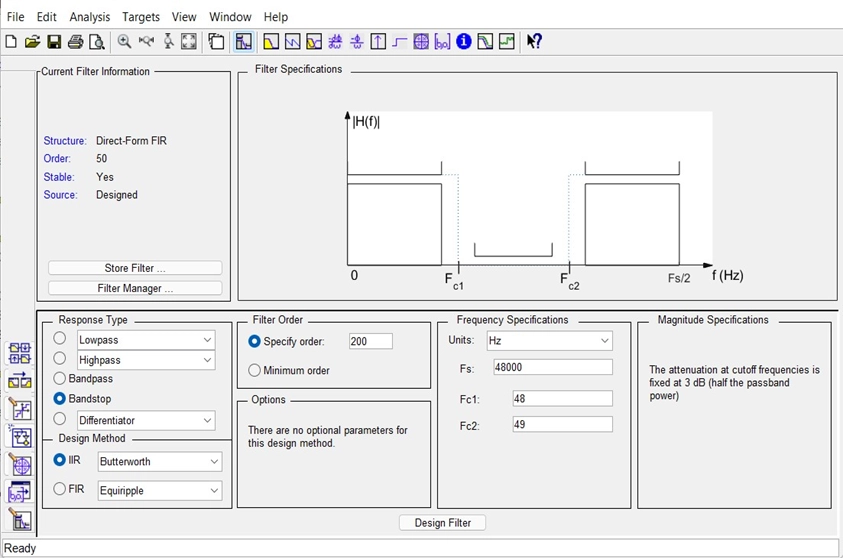
· Filter design user interface for selected frequency
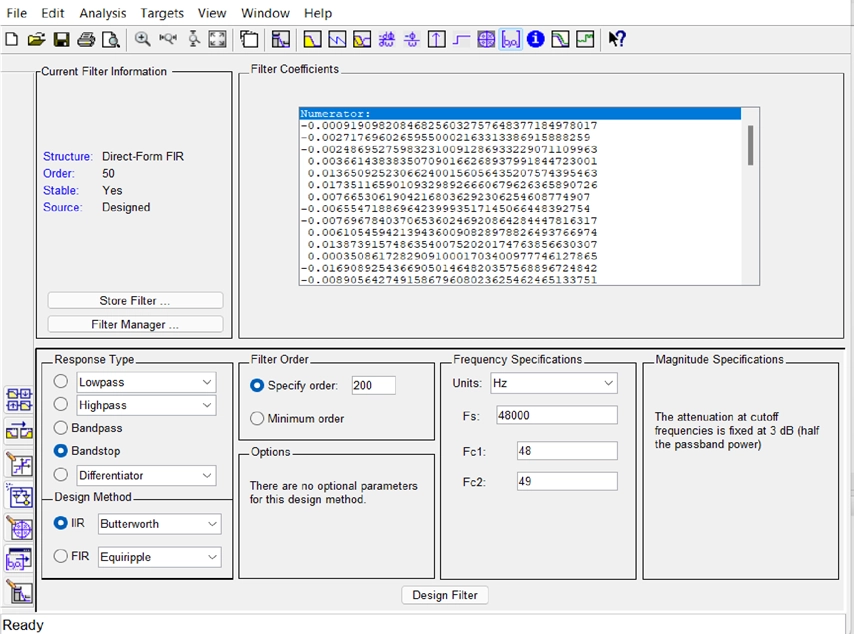
· Filter coefficients in Butterworth Band Stop Filters
A. Using Weiner Filters
Procedure:
1. Load the audio file and extract the audio signal
The code starts by loading the audio file using the audioread function and extracting the audio signal from the file. The audio signal is stored in the y variable, and the sampling frequency is stored in the Fe variable.
2. Extract the noise spectrum of the vuvuzela sound
The code extracts the noise spectrum of the vuvuzela sound from the audio signal using a time interval specified by t_min and t_max. The code computes the STFT of the audio signal using the spectrogram function and then computes the average spectrum of the vuvuzela sound over the specified time interval.
3. Estimate the SNR of the audio signal
The code estimates the SNR of the audio signal using the noise spectrum of the vuvuzela sound obtained in step 2. The code computes the power spectrum of the audio signal using the STFT and then computes the SNR estimate based on the power spectrum and the noise spectrum. The code can perform either apriori or aposteriori SNR estimation, depending on the value of the apriori_SNR parameter.
4. Compute a time-frequency attenuation map
The code computes a time-frequency attenuation map based on the SNR estimate computed in step 3. The attenuation map is computed using the an_lk formula, which is a function of the SNR estimate and several parameters, including the lambda, beta1, and beta2 parameters.
5. Apply a Wiener filter to the STFT of the audio signal
The code applies a Wiener filter to the STFT of the audio signal to obtain a denoised STFT. The Wiener filter is applied using the smoothed SNR estimate computed in step 3 and the H formula, which is a function of the smoothed SNR estimate.
6. Compute the inverse STFT of the denoised STFT
The code computes the inverse STFT of the denoised STFT to obtain the denoised audio signal. The code uses the ifft function to compute the inverse STFT and applies an overlapping-add technique to reconstruct the audio signal.
7. Display the original and denoised audio signals and spectrograms: The code displays the original and denoised audio signals and spectrograms using the plot and pcolor functions. The code also adds labels and titles to the plots to provide context.
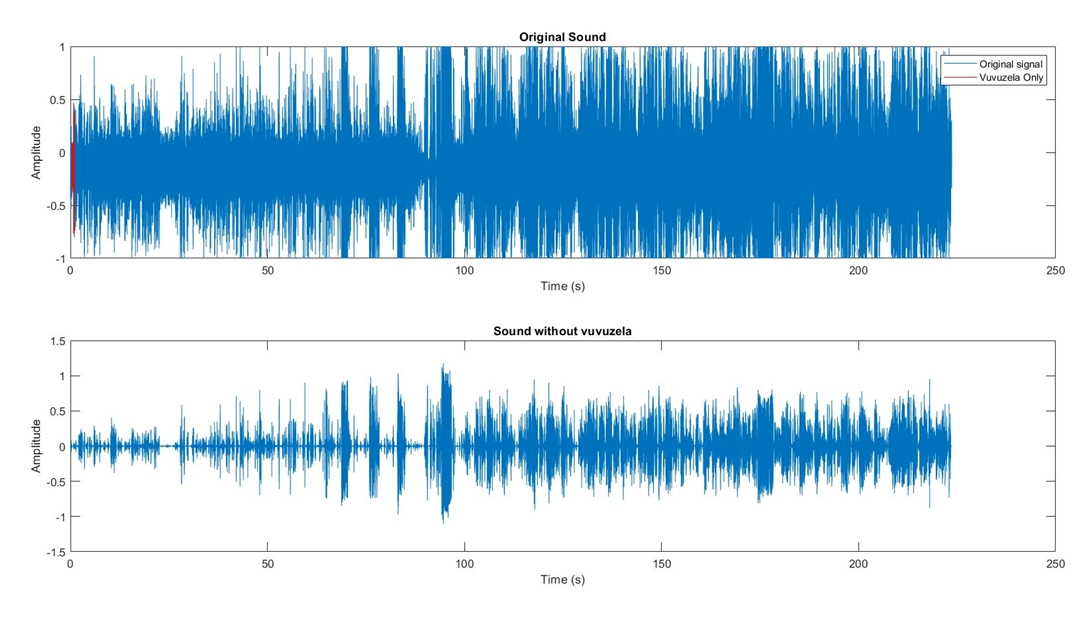
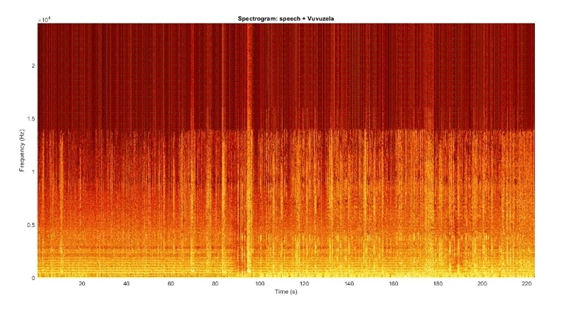
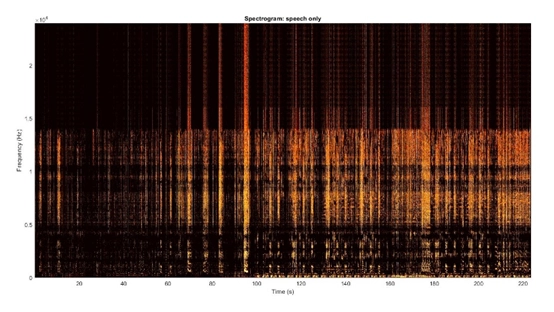
8. Play the original and denoised audio signals and save the denoised audio as a new file: The code plays the original and denoised audio signals using the sound function and saves the denoised audio signal as a new file using the audiowrite function. The code also includes some normalization and scaling factors to adjust the amplitude of the audio signal.
When considering the derived filter coefficients used in this Weiner filter method,
· High-pass filter:
The high-pass filter is designed using the Finite Impulse Response filter design method. The fir1 function is used to design the filter coefficients based on the desired cutoff frequency and filter order. The cutoff frequency is specified as a fraction of the Nyquist frequency, which is half the sampling frequency Fe. The filter order determines the number of filter coefficients and the steepness of the filter's frequency response. A higher filter order generally results in a steeper filter roll-off but also requires more computational resources.
· Wiener filter:
The Wiener filter is a linear filter that is commonly used for noise reduction and signal enhancement. The filter coefficients are based on the Signal to Noise Ratio or SNR estimate of the audio signal. The H formula is used to compute the filter coefficients, which are then applied to the STFT of the audio signal. The Wiener filter is designed to minimize the mean square error between the denoised signal and the original signal, given the SNR estimate.
The Wiener filter can be further improved by smoothing the filter coefficients using the filter function with a smoothing factor specified by the alpha_wiener parameter. The smoothing factor determines the strength of the smoothing and can be adjusted to balance between noise reduction and signal preservation. A higher smoothing factor generally results in a smoother filter response but also reduces the filter's ability to remove noise.
A Wiener filter is an adaptive filter. An adaptive filter is a filter that adjusts its parameters based on the input signal and the desired output signal. In the case of the Wiener filter, the filter coefficients are adjusted based on the SNR estimate of the input signal. The SNR estimate can be computed from the power spectrum of the input signal and the power spectrum of the noise. The Wiener filter is designed to minimize the mean square error between the filtered signal and the original signal, given the SNR estimate. The adaptive nature of the Wiener filter is what makes it effective for reducing noise in audio signals. The filter coefficients are adjusted based on the specific characteristics of the input signal and the noise, allowing the filter to adapt to changes in the signal and noise over time. This results in a more accurate and effective noise reduction compared to static filters, which have fixed filter coefficients that do not change based on the input signal.
References
[1] S. Boll, "Suppression of Acoustic Noise in Speech Using Spectral Subtraction," IEEE Transactions on Signal Processing, pp. pp 113-120, 1979.
[2] D. Malah and Y. Ephraim, "Speech enhancement using a minimum mean square error short-time spectral amplitude estimator," IEEE. Transactions in Acoust, Speech, Signal Process, vol. 32, no. December, pp. 1109 - 1121, 1984.
[3] S. Mallat, "A Wavelet Tour of Signal Processing," Academic Press, vol. 3rd, 2008.